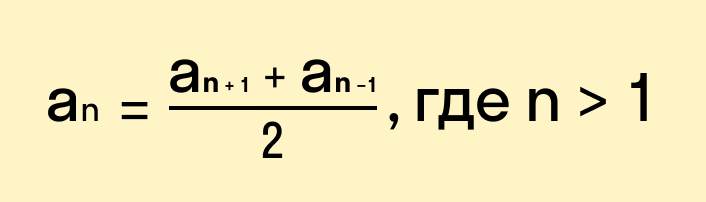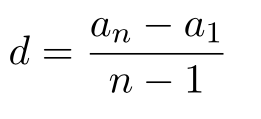Каждый член арифметической прогрессии отличный от первого

Если учишься в школе, то сто процентов учителя говорили про геометрическую и арифметическую прогрессии. Но у многих школьников возникает легкое непонимание этой темы «Арифметическая прогрессия» — не потому что она сложная, а потому что обычно ее слишком мало дают по программе.

Разность арифметической прогрессии

В этом материале расскажем самое главное об арифметической прогрессии. Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер. Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей. Возрастающие и убывающие последовательности называют монотонными последовательностями.

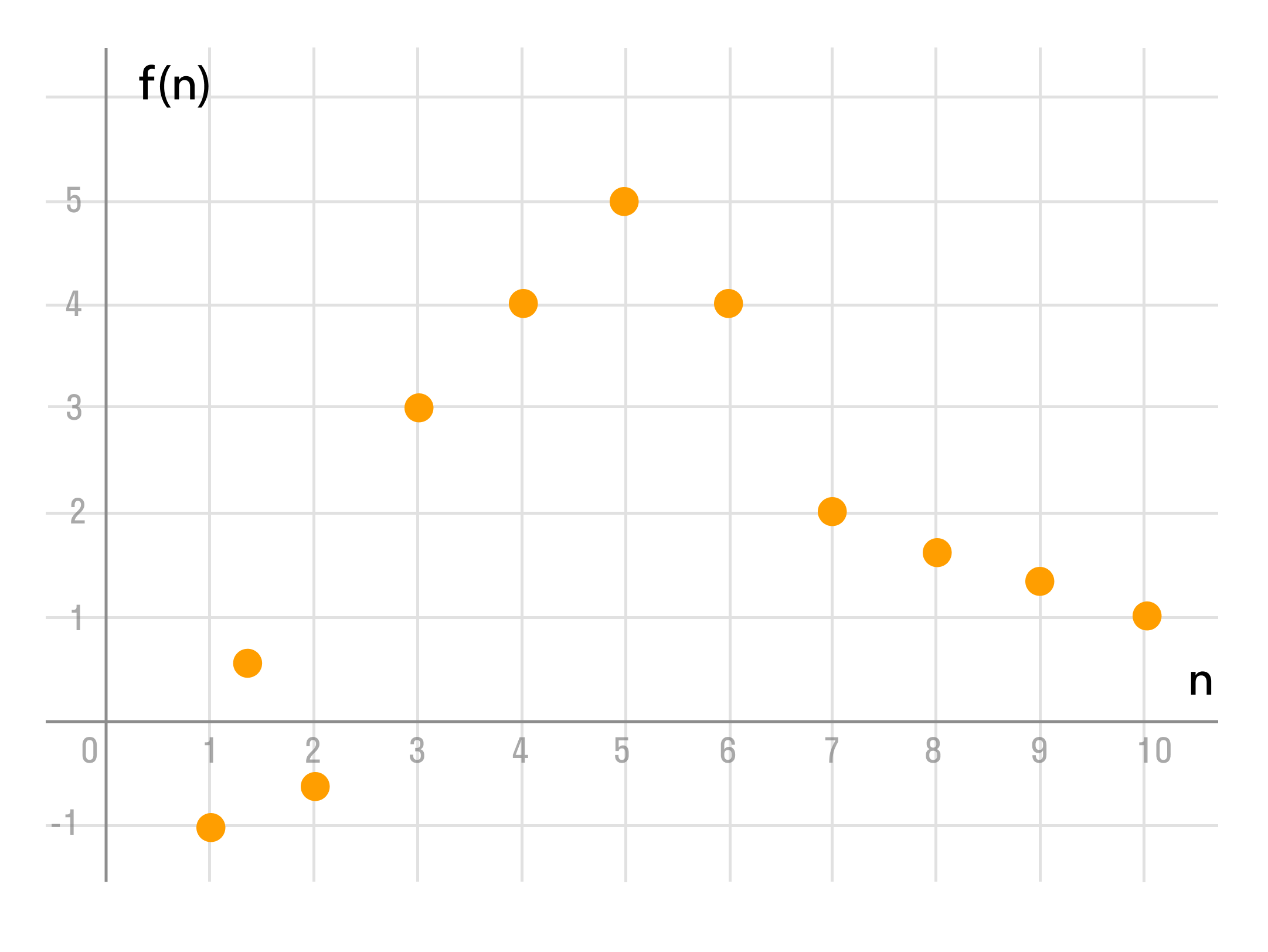
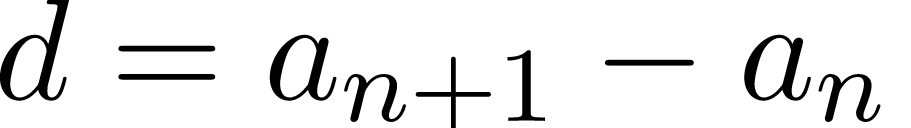
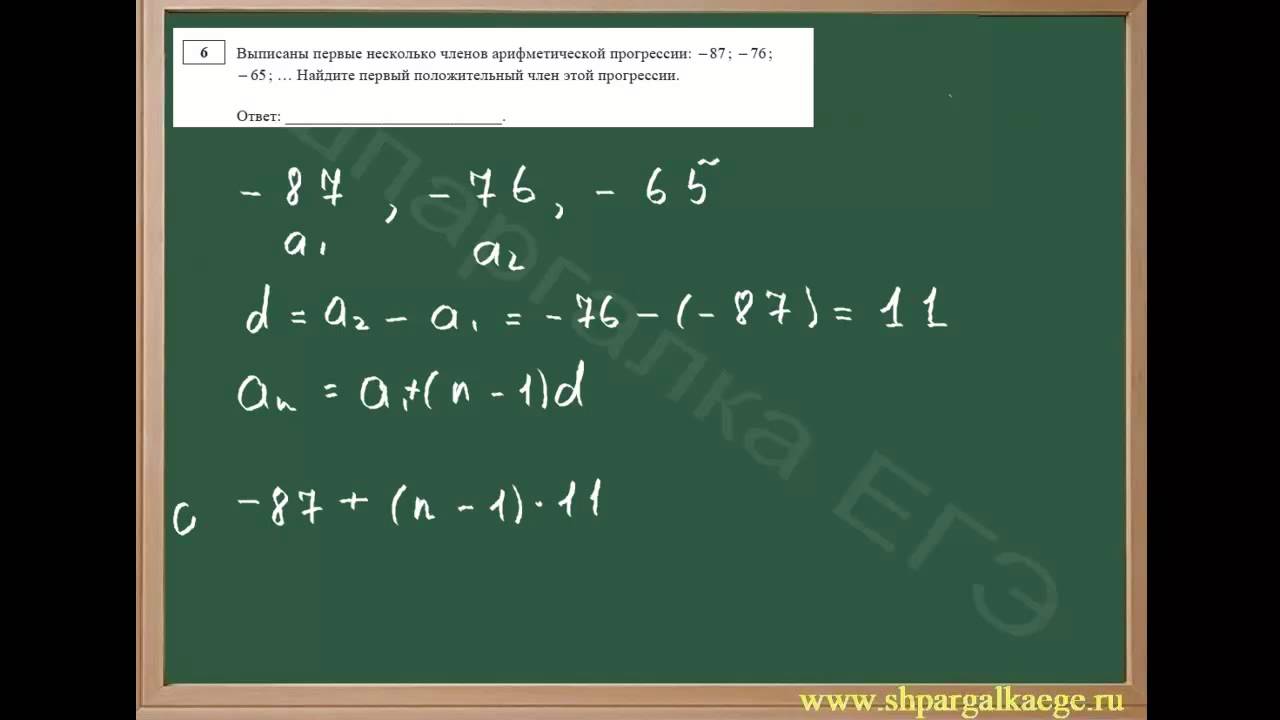
Задача отсюда:. Берем в рассмотрение первое условие задачи «Сумма трех чисел, составляющих убывающую арифметическую прогрессию, равна 24». Пусть a 1, a 2, a 3 — первые три члена арифметической прогрессии. Так как прогрессия бывающая, то можно записать их так:.

• Математически верная формулировка
• Любой член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому, т. Арифметическая прогрессия является монотонной последовательностью.
• Разделы: Математика. Оборудование: Электронный учебник, интерактивная доска, презентационные слайды с использованием мультимедий.
• Главный редактор И. Виноградов Редакционная коллегия: С.

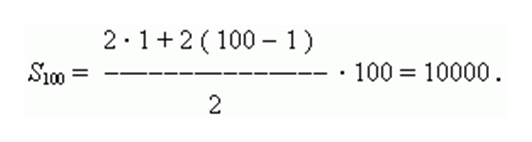
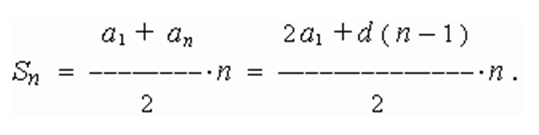
	349	Прогрессия - последовательность чисел, получаемых по некоторому правилу. Числа составляющие последовательность, называются ее членами.
	443	Мы уже рассказывали в наших задачах про числовые ряды — бесконечные суммы элементов различных последовательностей см.
	85	Какие из следующих утверждений правильны? Как видно, условие выполняется, а значит утверждение, что указанные выражения являются членами арифметической прогрессии, верно.
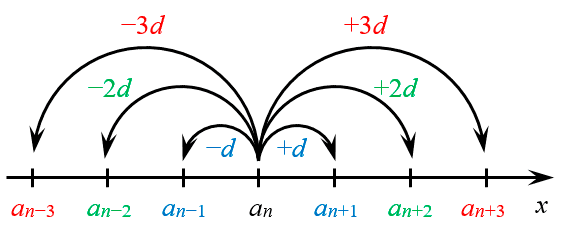
	395	Опишем словами эту формулу: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d. В этой числовой последовательности каждый следующий член равен предыдущему, сложенному с одним и тем же числом: 2.
	285	Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d , называется арифметической прогрессией.
	241	Пользуясь данным сайтом, вы даете свое согласие на использование файлов cookies.
	109	Related slideshows королькова а.
	298	Какие из следующих утверждений неправильны? Как видно, равенство не выполняется, а значит утверждение, что указанные выражения являются членами арифметической прогрессии, неверно.
	130	Прогрессия - это ряд чисел, каждый член которого зависит от предыдущего по общему для всего ряда закону.
	18	Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d , называется арифметической прогрессией. Число d называется разностью арифметической прогрессии.

Арифметические последовательности играют ключевую роль в различных математических и вычислительных задачах. В этой статье мы рассмотрим, как вычислить арифметические последовательности с использованием Python, используя итеративный подход. Мы предоставим подробные инструкции, практический пример и мини-проект для укрепления вашего понимания. Арифметическая последовательность представляет собой сумму членов арифметической прогрессии, где каждый член отличается от предыдущего на постоянное значение, известное как общая разность. Формула для нахождения суммы арифметической последовательности выглядит следующим образом:.

Похожие статьи

• Происшествия г алматы 24 11 2011 член опг
• Секс видео домашнее первый раз в попу
• Порно картинки большого члена
• Половой член длиной 25 см в пизде