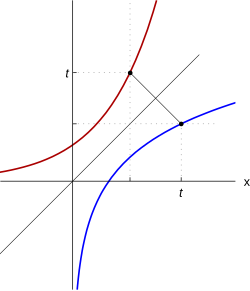
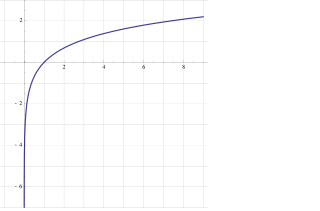
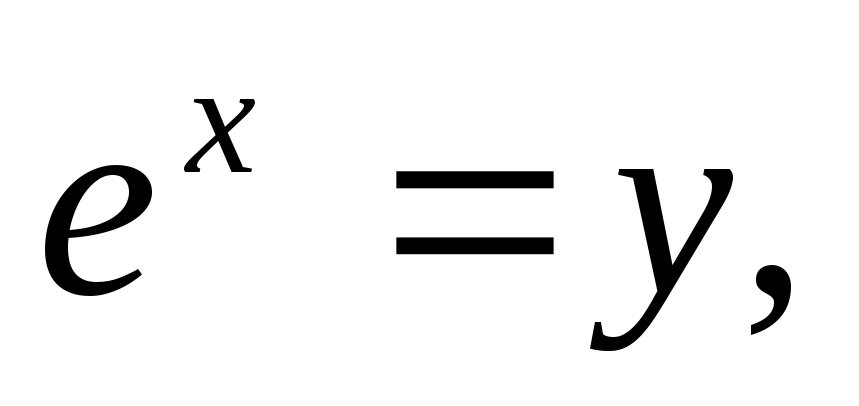Значения натурального логарифма 1

Натуральный логарифм является частным случаем логарифма, основанием которого является e. Любое неотрицательное число в том числе e , в степени 0 будет равняться 1.

Натуральный логарифм числа

Как и экспонента, логарифмическая функция относится к категории трансцендентных функций. Натуральные логарифмы полезны для решения алгебраических уравнений , в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. В приложениях натуральный логарифм участвует в математическом описании таких процессов, в которых скорость изменения некоторого количества в каждый момент обратно пропорциональна самому количеству. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества : чем больше атомов распадается, тем меньше их становится и тем медленнее идёт дальнейший процесс. Натуральные логарифмы играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения различных задач, например, нахождение сложных процентов.

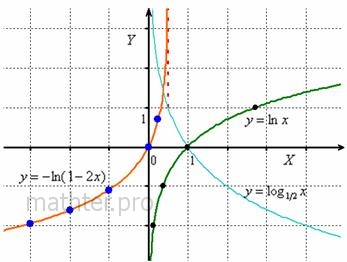
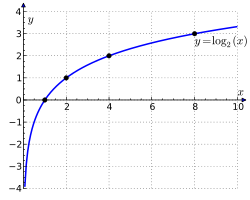
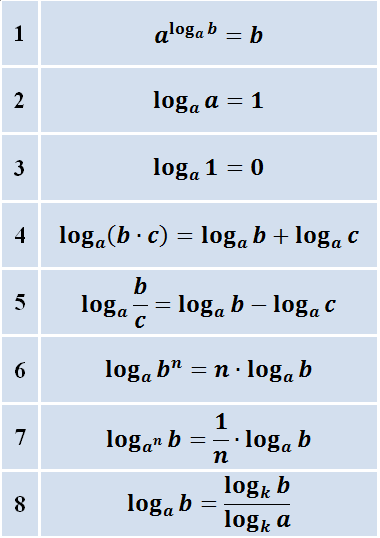
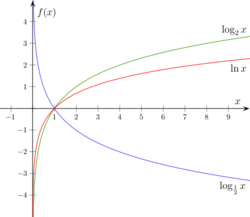
Содержание переместить в боковую панель скрыть. Логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Числа a и b чаще всего бывают вещественными, также существует теория комплексных логарифмов. Логарифмы обладают уникальными свойствами и их начали использовать для существенного упрощения трудоёмких вычислений.

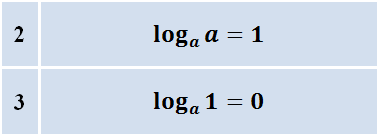
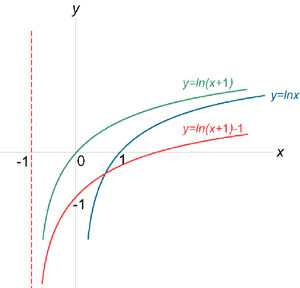
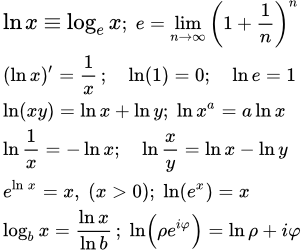
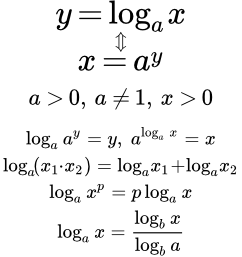
Регистрация Вход. Ответы Mail. Вопросы - лидеры.

Похожие статьи

• Методы продвижения натурального сока на рынке
• Сексуальное значение имени гузель
• Задано натуральное число а является ли оно кратным 7
• Порно с пухленькими большие натуральные сиськи